El sisè problema de la saga de problemes d'El País (quina iniciativa més bona!) era el següent:
http://www.elpais.com/articulo/sociedad/salvar/seguro/29/presos/elpepusoc/20110426elpepusoc_4/Tes
Podeu trobar la resposta i problemes semblants a aquest a la pàgina de la Wikipedia "Prisioners and hats puzzle":
http://en.wikipedia.org/wiki/Prisoners_and_hats_puzzle
dilluns, 25 d’abril del 2011
Inducció transfinita
Extret del llibre Teoría de Conjuntos y temas afines, de Seymour Lipschutz, pàg. 173
Definició:
Sigui A un conjunt ben ordenat i a un element de A. La secció inicial de a, "s(a)")
, és el conjunt d'elements de A estrictament anteriors a a.
Demostrar el principi d'inducció transfinita:
Principi d'inducció transfinita:
Donat un subconjunt S d'un conjunt ben ordenat A amb les següents propietats:
(1)
(2) \subset S$ "$s(a) \subset S$")
implica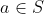 
Llavors es té que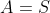
.
Demostració:
Suposem que
, és a dir que 
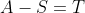és no buit. Com que A és ben ordenat, T té un primer element 
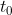. Tot element  "x \in s(t_0)")
és anterior a 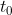i per tant no pot pertànyer a T, pertanyent per tant a S. Per tant tenim que  \subset S "s(t_0) \subset S")
. Per (2), tenim que 
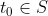, cosa que contradiu que 
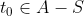. Per tant, la suposició que és falsa, és a dir, 
.
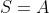Definició:
Sigui A un conjunt ben ordenat i a un element de A. La secció inicial de a,
Demostrar el principi d'inducció transfinita:
Principi d'inducció transfinita:
Donat un subconjunt S d'un conjunt ben ordenat A amb les següents propietats:
(1)
(2)
Llavors es té que
Demostració:
Suposem que
dimarts, 19 d’abril del 2011
5 - Un país d'escuradents
El cinquè problema de la sèrie d'El País, corresponent als dies 15-18 d'abril, el podeu veure aquí:
http://www.elpais.com/articulo/sociedad/ganar/siempre/palillos/elpepusoc/20110419elpepusoc_5/Tes
A continuació presentem la nostra solució als dos problemes que es proposaven.
.
.
.
Observación
===========
En total hay 19 palillos, distribuidos de la siguiente forma:
- 5 en la letra P
- 5 en la letra A
- 4 en la letra I
- 5 en la letra S
Solución al problema 1
======================
El jugador 1 gana siempre con la estrategia que explicamos a continuación:
La idea es que siempre, después de escoger el jugador 1, quede en la mesa una cantidad múltiple de 4 de palillos: 0, 4, 8, 12 o 16.
- Inicialmente el jugador coge 3. Así quedarán en la mesa 16.
- Después de qe el jugador 2 coja sus palillos, el jugador 1 cogerá la cantidad necesaria para que queden 12 en la mesa. Es decir,
* Si el jugador 2 coge 1, el jugador 1 coge 3
* Si el jugador 2 coge 2, el jugador 1 coge 2
* Si el jugador 2 coge 3, el jugador 1 coge 1
- Se repite el mismo proceso para que queden 8, 4 y 0 en la mesa. En este último caso, el jugador 1 habrá cogido siempre el últmo
palillo y por tanto ganará.
Solución al problema 2
======================
Definimos turno como una toma de palillos por parte de un jugador cualquiera, y recordamos que en un turno sólo se pueden coger palillos de una letra.
Definimos toma de una letra como un turno en el que se cogen palillos de esta letra.
El jugador 1 gana siempre con la estrategia que explicamos a continuación:
El jugador 1 tiene que asegurarse que las letras P, A y S se terminen exactamente en tres turnos (y tomas) y que la letra I se termine en dos turnos (y tomas). Si consigue que se cumpla esto habrá ganado, ya que las letras se terminarán en 3 + 3 + 2 + 3 = 11 turnos, y puesto que el jugador 1 tiene los turnos impares, él será el que coja el último palillo en el turno 11.
Veamos que puede conseguir esto:
- Si en el turno anterior el jugador 2 realiza la primera toma de una letra, en el siguiente turno el jugador 1 hará lo siguiente:
* Si la letra es P,A o S, cogerá todos los palillos menos 1, asegurando que la letra se termine en 3 tomas.
* Si la letra es la I, cogerá todos los palillos, asegurando que la letra se termine en 2 tomas.
Vemos que siempre puede hacer esto ya que en las letras P,A y S quedarán entre 2 y 4 palillos antes de su turno, y en la letra I quedarán entre 1 y 3 palillos antes de su turno.
- Si en el turno anterior el jugador 2 realiza la segunda toma de una letra que es P, A o S, en el siguiente turno el jugador 1 hará lo siguiente:
* Cogerá todos los palillos restantes, asegurando que la letra se termine en 3 tomas.
Vemos que siempre puede hacer esto ya que si el jugador 2 ha realizado la segunda toma de P, A o S sólo puede ser debido a que el jugador 1 habrá realizado la primera, y el jugador 1 habrá dejado 4 palillos pendientes (Ver el punto siguiente). Después de la toma del jugador 2, quedarán como mucho 3, y el jugador 1 podrá terminar la letra.
- Sino, el jugador 1 puede jugar cualquier opción válida de las siguientes en un turno:
* Realizar la primera toma de las letras P, A o S cogiendo 1 palillo.
* Realizar la primera toma de I cogiendo 3 palillos.
* Realizar la segunda toma de P, A o S dejando sólo uno.
* Realizar la segunda toma de I cogiendo todos los palillos restantes.
* Realizar la tercera toma de P, A o S cogiendo los palillos restantes.
Vemos que con todos estos movimientos el jugador 1 avanza en la resolución del problema manteniendo los turnos y tomas previstos. Y también vemos que el jugador 2 no tiene ninguna posibilidad de variar ni el número de turnos ni el número de tomas en el que se terminan las letras.
http://www.elpais.com/articulo/sociedad/ganar/siempre/palillos/elpepusoc/20110419elpepusoc_5/Tes
A continuació presentem la nostra solució als dos problemes que es proposaven.
.
.
.
Observación
===========
En total hay 19 palillos, distribuidos de la siguiente forma:
- 5 en la letra P
- 5 en la letra A
- 4 en la letra I
- 5 en la letra S
Solución al problema 1
======================
El jugador 1 gana siempre con la estrategia que explicamos a continuación:
La idea es que siempre, después de escoger el jugador 1, quede en la mesa una cantidad múltiple de 4 de palillos: 0, 4, 8, 12 o 16.
- Inicialmente el jugador coge 3. Así quedarán en la mesa 16.
- Después de qe el jugador 2 coja sus palillos, el jugador 1 cogerá la cantidad necesaria para que queden 12 en la mesa. Es decir,
* Si el jugador 2 coge 1, el jugador 1 coge 3
* Si el jugador 2 coge 2, el jugador 1 coge 2
* Si el jugador 2 coge 3, el jugador 1 coge 1
- Se repite el mismo proceso para que queden 8, 4 y 0 en la mesa. En este último caso, el jugador 1 habrá cogido siempre el últmo
palillo y por tanto ganará.
Solución al problema 2
======================
Definimos turno como una toma de palillos por parte de un jugador cualquiera, y recordamos que en un turno sólo se pueden coger palillos de una letra.
Definimos toma de una letra como un turno en el que se cogen palillos de esta letra.
El jugador 1 gana siempre con la estrategia que explicamos a continuación:
El jugador 1 tiene que asegurarse que las letras P, A y S se terminen exactamente en tres turnos (y tomas) y que la letra I se termine en dos turnos (y tomas). Si consigue que se cumpla esto habrá ganado, ya que las letras se terminarán en 3 + 3 + 2 + 3 = 11 turnos, y puesto que el jugador 1 tiene los turnos impares, él será el que coja el último palillo en el turno 11.
Veamos que puede conseguir esto:
- Si en el turno anterior el jugador 2 realiza la primera toma de una letra, en el siguiente turno el jugador 1 hará lo siguiente:
* Si la letra es P,A o S, cogerá todos los palillos menos 1, asegurando que la letra se termine en 3 tomas.
* Si la letra es la I, cogerá todos los palillos, asegurando que la letra se termine en 2 tomas.
Vemos que siempre puede hacer esto ya que en las letras P,A y S quedarán entre 2 y 4 palillos antes de su turno, y en la letra I quedarán entre 1 y 3 palillos antes de su turno.
- Si en el turno anterior el jugador 2 realiza la segunda toma de una letra que es P, A o S, en el siguiente turno el jugador 1 hará lo siguiente:
* Cogerá todos los palillos restantes, asegurando que la letra se termine en 3 tomas.
Vemos que siempre puede hacer esto ya que si el jugador 2 ha realizado la segunda toma de P, A o S sólo puede ser debido a que el jugador 1 habrá realizado la primera, y el jugador 1 habrá dejado 4 palillos pendientes (Ver el punto siguiente). Después de la toma del jugador 2, quedarán como mucho 3, y el jugador 1 podrá terminar la letra.
- Sino, el jugador 1 puede jugar cualquier opción válida de las siguientes en un turno:
* Realizar la primera toma de las letras P, A o S cogiendo 1 palillo.
* Realizar la primera toma de I cogiendo 3 palillos.
* Realizar la segunda toma de P, A o S dejando sólo uno.
* Realizar la segunda toma de I cogiendo todos los palillos restantes.
* Realizar la tercera toma de P, A o S cogiendo los palillos restantes.
Vemos que con todos estos movimientos el jugador 1 avanza en la resolución del problema manteniendo los turnos y tomas previstos. Y también vemos que el jugador 2 no tiene ninguna posibilidad de variar ni el número de turnos ni el número de tomas en el que se terminan las letras.
dimarts, 12 d’abril del 2011
4 - Un rellotge de dos colors
El quart problema del concurs del diari El País, corresponent als dies 8-11 d'abril, era el següent:
http://www.elpais.com/videos/sociedad/reloj/colores/elpepueco/20110407elpepusoc_1/Ves/
La solució es va publicar en aquesta pàgina:
http://www.elpais.com/articulo/sociedad/Siempre/hay/recta/cualquier/reloj/elpepueco/20110412elpepusoc_11/Tes
En aquest escrit presentem la solució que vam enviar.
.
.
.
Empezamos la demostración con una observación:
Observación
===========
Sea una línea que separa seis números de otros seis, y que en un lado deja x números pintados de azul y (6-x) pintados de rojo.
Consideramos ahora otra línea separadora que mantenga en el mismo lado a cinco de los seis números anteriores y añada un nuevo número. Es decir, si antes la línea separaba
1 2 3 4 5 6 | 7 8 9 10 11 12
ahora esta puede ser
12 1 2 3 4 5 | 6 7 8 9 10 11
o
2 3 4 5 6 7 | 8 9 10 11 12 1.
Estas nuevas separaciones dejan en el mismo lado a x+1,x o x-1 números azules y (6-x)+1, (6-x) o (6-x)-1 pintados de rojo.
demostración
============
Es sencillo:
- Si el color del número que ahora no está coincide con el del nuevo número, seguirá habiendo x números azules y (6-x) de rojos.
- Si el número que ahora no está es azul y el nuevo es rojo, ahora habrá x-1 números azules y (6-x)+1 de rojos.
- Si el número que ahora no esta es rojo y el nuevo es azul, ahora habrá x+1 números azules y (6-x)-1 de rojos.
Con esta observación ya podemos demostrar el problema.
demostración del problema
=========================
Supongamos que no es cierto, es decir, que existe una configuración de seis números azules y seis rojos que no se pueden separar dejando tres de cada color en cada lado.
Trazamos una línea que separe los puntos
1 2 3 4 5 6 | 7 8 9 10 11 12
Ahora tendremos x bolas azules en el lado de los números (1 2 3 4 5 6).
Supongamos x > 3 (x = 3 no puede ser, y si x < 3 cambiamos azules por rojas en el razonamiento). 1 2 3 4 5 6 | 7 8 9 10 11 12 > 3 azules
Consideramos ahora la separación
2 3 4 5 6 7 | 8 9 10 11 12 1
Por la observación anterior, en el lado de los números (2 3 4 5 6 7) podrían estar 3 o más de 3 bolas azules. Pero 3 no puede haber, ya que entonces tendríamos una solución. Por tanto, sigue habiendo más de 3:
2 3 4 5 6 7 | 8 9 10 11 12 1
> 3 azules
Razonando de igual modo, podemos construir las separaciones
3 4 5 6 7 8 | 9 10 11 12 1 2
> 3 azules
4 5 6 7 8 9 | 10 11 12 1 2 3
> 3 azules
...
Hasta que llegamos a la configuración
7 8 9 10 11 12 | 1 2 3 4 5 6
> 3 azules
que da lugar a una contradicción con la primera configuración, ya que
- El reloj tiene 6 números azules.
- Tenemos más de 3 azules en el lado de los números (1 2 3 4 5 6) y más de 3 azules en el lado de los números (7 8 9 10 11 12)!!!
Por tanto, para toda configuración del reloj existe una separación que deja 3 números azules y 3 de rojos en cada lado.
http://www.elpais.com/videos/sociedad/reloj/colores/elpepueco/20110407elpepusoc_1/Ves/
La solució es va publicar en aquesta pàgina:
http://www.elpais.com/articulo/sociedad/Siempre/hay/recta/cualquier/reloj/elpepueco/20110412elpepusoc_11/Tes
En aquest escrit presentem la solució que vam enviar.
.
.
.
Empezamos la demostración con una observación:
Observación
===========
Sea una línea que separa seis números de otros seis, y que en un lado deja x números pintados de azul y (6-x) pintados de rojo.
Consideramos ahora otra línea separadora que mantenga en el mismo lado a cinco de los seis números anteriores y añada un nuevo número. Es decir, si antes la línea separaba
1 2 3 4 5 6 | 7 8 9 10 11 12
ahora esta puede ser
12 1 2 3 4 5 | 6 7 8 9 10 11
o
2 3 4 5 6 7 | 8 9 10 11 12 1.
Estas nuevas separaciones dejan en el mismo lado a x+1,x o x-1 números azules y (6-x)+1, (6-x) o (6-x)-1 pintados de rojo.
demostración
============
Es sencillo:
- Si el color del número que ahora no está coincide con el del nuevo número, seguirá habiendo x números azules y (6-x) de rojos.
- Si el número que ahora no está es azul y el nuevo es rojo, ahora habrá x-1 números azules y (6-x)+1 de rojos.
- Si el número que ahora no esta es rojo y el nuevo es azul, ahora habrá x+1 números azules y (6-x)-1 de rojos.
Con esta observación ya podemos demostrar el problema.
demostración del problema
=========================
Supongamos que no es cierto, es decir, que existe una configuración de seis números azules y seis rojos que no se pueden separar dejando tres de cada color en cada lado.
Trazamos una línea que separe los puntos
1 2 3 4 5 6 | 7 8 9 10 11 12
Ahora tendremos x bolas azules en el lado de los números (1 2 3 4 5 6).
Supongamos x > 3 (x = 3 no puede ser, y si x < 3 cambiamos azules por rojas en el razonamiento). 1 2 3 4 5 6 | 7 8 9 10 11 12 > 3 azules
Consideramos ahora la separación
2 3 4 5 6 7 | 8 9 10 11 12 1
Por la observación anterior, en el lado de los números (2 3 4 5 6 7) podrían estar 3 o más de 3 bolas azules. Pero 3 no puede haber, ya que entonces tendríamos una solución. Por tanto, sigue habiendo más de 3:
2 3 4 5 6 7 | 8 9 10 11 12 1
> 3 azules
Razonando de igual modo, podemos construir las separaciones
3 4 5 6 7 8 | 9 10 11 12 1 2
> 3 azules
4 5 6 7 8 9 | 10 11 12 1 2 3
> 3 azules
...
Hasta que llegamos a la configuración
7 8 9 10 11 12 | 1 2 3 4 5 6
> 3 azules
que da lugar a una contradicción con la primera configuración, ya que
- El reloj tiene 6 números azules.
- Tenemos más de 3 azules en el lado de los números (1 2 3 4 5 6) y más de 3 azules en el lado de los números (7 8 9 10 11 12)!!!
Por tanto, para toda configuración del reloj existe una separación que deja 3 números azules y 3 de rojos en cada lado.
dissabte, 9 d’abril del 2011
3 - Un quadrat màgic de productes
El tercer problema del concurs d'El País, corresponent als dies 1-4 d'abril, era el següent:
http://www.elpais.com/videos/sociedad/cuadrado/magico/productos/elpepusoc/20110401elpepusoc_1/Ves/
Es tracta de construir un quadrat 3x3 amb nombres enters positius i diferents tals que
http://www.elpais.com/articulo/sociedad/Cuadrado/magico/productos/solucionado/elpepusoc/20110405elpepusoc_2/Tes
Nosaltres, aquí, expliquem la que vam trobar.
Construir quadrats màgics amb sumes és relativament fàcil, aquí en tenim un exemple:
4 9 2
3 5 7
8 1 6
i transformar un quadrat en un altre mitjançant sumes i restes és senzill també. Aquí tenim un altre quadrat màgic que és com l'anterior però restant 4 a cada nombre:
La idea que vam pensar és transformar el problema del quadrat màgic de productes en un problema de quadrats màgics amb sumes. Com? Jugant amb els exponents!
El primer intent que vam fer fou construir un quadrat on tots els números fossin 15^x,
amb x un exponent diferent. Com que al mig hi ha d'haver el número 15, la proposta era el següent quadrat:
Bé! ara ja teníem un quadrat màgic de productes amb el número 15 al mig, tot i que no era correcte perquè no tots els números eren enters positius.
La següent idea que vam pensar és en jugar amb els exponents però descomposant el número 15 en els seus factors: 3 i 5
15 = 3^1 * 5^1
Llavors el problema era el següent:
Construir un quadrat màgic de sumes de parells de nombres on
on el primer nombre dels parells és l'exponent del 3 i el segon l'exponent del 5.
Aquest problema és una mica més complicat que el dels quadrats màgics de sumes, però amb una mica de paciència es pot trobar una solució. Per exemple:
2/1 0/0 1/2
0/2 1/1 2/0
1/0 2/2 0/1
que correspon al quadrat màgic de productes
Bé! Ja teníem una solució!
Després ens vam preguntar perquè en el plantejament del problema es posava el número 15 al mig. Existeix una solució semblant amb un número més petit al centre del quadrat?
Sí, posant-hi el 6. El 6 és el número més petit compost producte de dos números diferents que no siguin l'1. Amb el 6 al mig del quadrat i mantenint els exponents anteriors tenim un altre quadrat màgic de productes.
http://www.elpais.com/videos/sociedad/cuadrado/magico/productos/elpepusoc/20110401elpepusoc_1/Ves/
Es tracta de construir un quadrat 3x3 amb nombres enters positius i diferents tals que
- A la casella del mig hi hagi el número 15
- El producte de les tres files, tres columnes i dues diagonals sigui sempre el mateix.
http://www.elpais.com/articulo/sociedad/Cuadrado/magico/productos/solucionado/elpepusoc/20110405elpepusoc_2/Tes
Nosaltres, aquí, expliquem la que vam trobar.
Construir quadrats màgics amb sumes és relativament fàcil, aquí en tenim un exemple:
4 9 2
3 5 7
8 1 6
i transformar un quadrat en un altre mitjançant sumes i restes és senzill també. Aquí tenim un altre quadrat màgic que és com l'anterior però restant 4 a cada nombre:
0 5 -2
-1 1 3
4 -3 2
La idea que vam pensar és transformar el problema del quadrat màgic de productes en un problema de quadrats màgics amb sumes. Com? Jugant amb els exponents!
El primer intent que vam fer fou construir un quadrat on tots els números fossin 15^x,
amb x un exponent diferent. Com que al mig hi ha d'haver el número 15, la proposta era el següent quadrat:
15^0 15^5 15^(-2)
15^(-1) 15^1 15^3
15^4 15^(-3) 15^2
Bé! ara ja teníem un quadrat màgic de productes amb el número 15 al mig, tot i que no era correcte perquè no tots els números eren enters positius.
La següent idea que vam pensar és en jugar amb els exponents però descomposant el número 15 en els seus factors: 3 i 5
15 = 3^1 * 5^1
Llavors el problema era el següent:
Construir un quadrat màgic de sumes de parells de nombres on
- La suma de cada parell de nombre sigui un quadrat màgic
- No es repeteixi el mateix parell de nombres
x/x x/x x/x
x/x 1/1 x/x
x/x x/x x/x
on el primer nombre dels parells és l'exponent del 3 i el segon l'exponent del 5.
Aquest problema és una mica més complicat que el dels quadrats màgics de sumes, però amb una mica de paciència es pot trobar una solució. Per exemple:
2/1 0/0 1/2
0/2 1/1 2/0
1/0 2/2 0/1
que correspon al quadrat màgic de productes
45 1 50
25 15 9
3 225 5
Bé! Ja teníem una solució!
Després ens vam preguntar perquè en el plantejament del problema es posava el número 15 al mig. Existeix una solució semblant amb un número més petit al centre del quadrat?
Sí, posant-hi el 6. El 6 és el número més petit compost producte de dos números diferents que no siguin l'1. Amb el 6 al mig del quadrat i mantenint els exponents anteriors tenim un altre quadrat màgic de productes.
Subscriure's a:
Missatges (Atom)