Extret del llibre Teoría de Conjuntos y temas afines, de Seymour Lipschutz, pàg. 173Definició:Sigui A un conjunt ben ordenat i a un element de A. La
secció inicial de a,
)
, és el conjunt d'elements de A estrictament anteriors a a.
Demostrar el principi d'inducció transfinita:
Principi d'inducció transfinita:Donat un subconjunt S d'un conjunt ben ordenat A amb les següents propietats:
(1)

(2)
 \subset S$)
implica
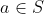
Llavors es té que
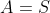
.
Demostració:Suposem que

, és a dir que
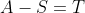
és no buit. Com que A és ben ordenat, T té un primer element
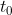
. Tot element
)
és anterior a
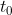
i per tant no pot pertànyer a T, pertanyent per tant a S. Per tant tenim que
 \subset S)
. Per (2), tenim que
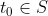
, cosa que contradiu que
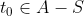
. Per tant, la suposició que

és falsa, és a dir,
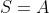
.
Cap comentari:
Publica un comentari a l'entrada